Juros compostos Matemática financeira Taxas de juros Todos os Artigos do Blog
Taxas Nominal, Efetiva, Proporcional e Equivalente – Explicação Passo a Passo
Neste artigo você vai aprender a identificar, diferenciar e calcular a taxa nominal, efetiva, proporcional e equivalente. Para isso vamos apresentar exemplos comuns e resolver eles passo a passo.
taxa nominal e efetiva
Que taxa é essa?
Nominal ou efetiva?
Realmente esta é uma dúvida muito comum dos alunos em cursos introdutórios de matemática financeira. Este tipo de conteúdo também é muito cobrado em concursos públicos. A chave para entender a diferença entre taxa nominal e efetiva está no período de capitalização.
No exemplo acima como temos uma taxa de 36 % ao ano só que capitalizada mensalmente. Dizemos que o período de capitalização desta taxa é mensal e que a taxa está em um período diferente do período de capitalização.
Ou seja, o prazo de referência da taxa é diferente do prazo de capitalização. O período de capitalização da taxa é, portanto, o prazo que vai ser aplicado efetivamente a taxa.
O que é Taxa Nominal
Sabendo o que é período de capitalização podemos definir o que é taxa nominal. Dizemos que taxa nominal é aquela taxa em que o prazo de referência para taxa é diferente do período de capitalização.
No exemplo temos 36 % ao ano com capitalização mensal. O prazo da taxa é ao ano só que não é igual ao prazo de capitalização, que é mensal. Assim sendo, esta taxa é uma taxa nominal.
Veja outros exemplos de taxa nominal:
- 24 % ao ano com capitalização bimestral
- 12 % ao semestre com capitalização mensal
- 5 % ao mês com capitalização diária.
As taxas nominais não deve ser usadas em cálculos financeiros pois não refletem efetivamente o valor do dinheiro no tempo através do regime de juros compostos.
Para que possamos trabalhar com elas precisamos converter elas em taxas efetivas.
Mas o que é taxa efetiva?
O que é Taxa efetiva
As taxas efetivas são aquelas taxa usadas “efetivamente” nos cálculos financeiros. Perece redundante não?
Mas é isso mesmo, as taxa efetivas são aquelas que realmente usamos nas fórmulas matemáticas do regime de juros compostos, modelo de juros usado na grande maioria das operações do mercado financeiro.
Uma taxa efetiva é aquela em que o período de referência da taxa é igual ao período de capitalização.
Por exemplo:
- 1 % ao mês com capitalização mensal
- 18 % ao ano com capitalização anual
- 8 % ao semestre com capitalização semestral
Para todos exemplos acima temos período de capitalização igual ao período da taxa. Assim, todas elas são taxas equivalentes.
Na prática não precisamos especificar o período de capitalização das taxas equivalestes. Se a taxa não apresenta o período de capitalização, interpretamos ela como taxa efetiva. Veja como ficaria a representação das taxa efetivas anteriores:
- 1 % am
- 18 % aa
- 8 % as
onde:
- am= ao mês
- aa = ao ano
- as = ao semestre
Sabendo que a taxa efetiva é a que deve ser usada nos cálculos financeiros, como transformar a taxa nominal em taxa efetiva?
Como transformar taxa nominal em taxa efetiva?
Vejamos o exemplo de taxa nominal que apresentamos no início deste artigo, 36% ao ano com capitalização mensal. Sabemos que essa taxa é uma taxa nominal, pois o período da taxa é diferente do período de capitalização.
Para transformar a taxa nominal em taxa efetiva precisamos dividir ela pelo número de períodos de capitalização.
Para uma taxa de 36 % ao ano com capitalização mensal, por exemplo. Teremos que dividir por 12, poi em um ano temos 12 meses, dessa forma encontramos a taxa efetiva mensal.
Então a taxa efetiva mensal de 36% ao ano com capitalização mensal será de:
Taxa efetiva mensal= 36/12 = 3% ao mês
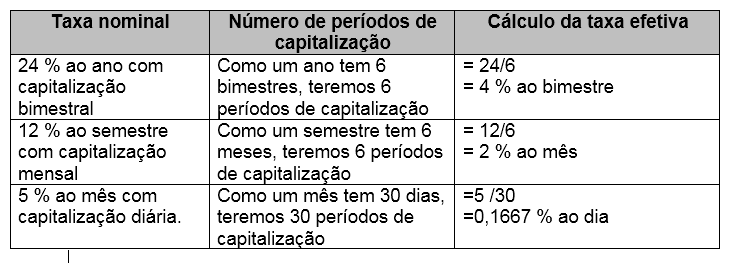
Outros exemplos:
Note como é fácil calcular a taxa efetiva a partir da taxa nominal, basta dividir pelo número de períodos de capitalização.
O que são taxas proporcionais
Agora que entendemos o que são taxas efetivas, vamos aprender o que são taxas proporcionais e taxas equivalentes.
No exemplo anterior você viu que a taxa de 36 % ao ano com capitalização mensal é uma taxa nominal. Quando dividimos pelo número de períodos de capitalização, encontramos a taxa efetiva mensal de 3 % ao mês.
Mas o que vem a ser taxa proporcional. Podemos afirmar que as taxas proporcionais são taxas múltiplas uma das outras. Este conceito considera que o valor dos juros é linear em consideração ao tempo.
Exemplos de taxas proporcionais:
- 36 % ao ano é proporcional a uma taxa de 18 % ao semestre. Pois 2 x18 = 36
- 24 % ao ano é proporcional a uma taxa de 2 % ao mês. Pois 12 *2 = 24
- 12 % ao semestre é proporcional a 2 % ao mês. Pois 6*2= 12
- 1% ao mês é proporcional a 6 % ao semestre que são proporcionais a 12 % ao ano.
Fácil não?
O que são taxas equivalentes
Duas taxas efetivas são ditas equivalentes se transformadas, utilizando as equações de juros, compostos para mesma unidade de tempo apresentam o mesmo valor.
Também podemos afirmar que as taxas equivalentes são aquelas que produzem o mesmo valor futuro aplicadas ao mesmo valor inicial.
A unica forma de encontrar taxas equivalentes é através da aplicação das fórmulas do regime de juros compostos.
Veremos a seguir um exemplo prático.
Por exemplo:
Qual seria a taxa equivalente anual de uma taxa de 15,49 % ao mês?
Para encontrar a taxa anual temos que utilizar a fórmula de equivalência da taxa mensal para anual:
Como temos uma taxa mensal de 15,49% ao mês, resolvendo para taxa anual, temos:
Ou seja, a taxa mensal de 15,49% ao mês é equivalente a uma taxa de 463,03% ao ano.
Lembramos que as taxa só podem ser ditas equivalentes se puderem ser convertidas através dessas fórmula de conversão de taxas de juros compostos:
Onde:
Vamos para outros exemplos para diferenciar as taxas proporcionais e efetivas:
- 24 % ao ano com capitalização anual é proporcional a 2 % ao mês com capitalização mensal, pois 2*12 = 24. O conceito de taxas proporcionais é utilizado em juros simples.
- 24 % ao ano com capitalização anual é equivalente a 1,808758 % ao mês. Pois um capital aplicado por 12 meses a taxa de 1,81 irá render 24 % ao ano. Este conceito é utilizado nos cálculos do regime de juros compostos.
Taxas Nominal, Efetiva, Proporcional e Equivalente – resumo
Segue abaixo um infográfico com resumo de tudo que foi visto no texto.
Quer saber mais sobre conversão e equivalência de taxas de juros compostos, veja este outro post no nosso blog:
http://calculadorajuroscompostos.com.br/converter-taxa-de-juros-compostos/
Compartilhe este texto links sociais logo abaixo!
Muito obrigado!


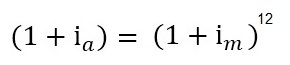
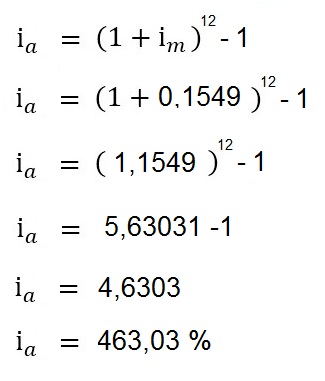
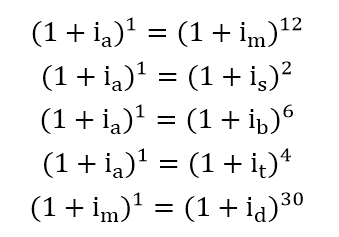





24 % ao ano com capitalização anual é equivalente a 1,808758 % ao mês. Pois um capital aplicado por 12 meses a taxa de 1,81 irá render 24 % ao ano. Este conceito é utilizado nos cálculos do regime de juros compostos.
COMO EU CALCULO ISSO…..]
Boa noite, venho por este meio a pedir ajuda de esplicacao de calculo financeiro
Oi Jeremias,
Qual a sua dúvida?