Convenção Linear e Exponencial – Exercícios Resolvidos

Neste artigo você vai aprender como calcular a Convenção Linear e Exponencial utilizando as fórmulas. Inicialmente iremos apresentar o que é o conceito de convenção da matemática financeira.

Em seguida vamos diferenciar a convenção linear da convenção exponencial. Por fim vamos ver dois exercícios resolvidos de convenção Linear e exponencial utilizando as fórmulas.

Seja muito bem vindo ao blog.

Se você gostar do conteúdo deste artigo pedimos que compartilhe ele em suas redes sociais, pois isso ajuda bastante a continuarmos a publicar textos como este.

Caso tenha alguma dúvida ou sugestão, basta entrar em contato através do formulário de contato ao final deste artigo.

O Que é Convenção na Matemática Financeira?

Vamos iniciar nosso estudo entendendo o que vem a ser o conceito de convenção da matemática financeira. Para que serve e em que situações utilizamos convenção.

Em algumas situações práticas da matemática financeira temo o prazo de pagamento ou de recebimento não inteiro, 2,5 meses por exemplo. Prazo este não inteiro  em relação ao prazo definido para a taxa, 5 % ao mês por exemplo.

Na prática este tipo de situação não é muito comum, mas pode acontecer. A não-formação dos juros em intervalos de tempo inferiores a um período inteiro pode ser solucionada através das chamadas convenções.

Inclusive este conteúdo é cobrado em alguns concursos públicos na área financeira, como para bancos por exemplo.

Temos dois modelos de convenções para este tipo de situação: Convenção Linear e a Convenção Exponencial.

O que é Convenção Linear?

Na Convenção Linear resolvemos esta situação utilizando uma mistura do regime composto e linear, usando a  formulas de juros compostos na parte inteira do período e  de juros simples na parte fracionária.

Veja a equação abaixo onde encontramos o montante (valor futuro) utilizando convenção linear.

Onde:

M= Montante

C= Capital

i = taxa de juros

n= Parte inteira do tempo

nfrac= Parte fracionada do tempo

Iremos resolver mais a frente neste artigo um exemplo passo a passo utilizando a fórmula de convenção linear.

O que é Convenção Exponencial?

Ao contrário da convenção linear, a convenção exponencial  utiliza o regime de capitalização para todo o período, tanto para parte inteira como para fracionada.

Este tipo de  convenção é mais usada na prática porque emprega o juros compostos e taxas equivalentes para as situações onde os períodos não são inteiros. Fazendo assim que o valor futuro se situe mais próximo da realidade.

Veja na equação abaixo a fórmula para encontrar o montante utilizando convenção exponencial.

Note que o n utilizando não diferencia parte inteira e fracionada, vamos detalhar melhor esta situação no exemplo mais a frente.

 

Convenção Linear e Exponencial – Exercícios Resolvidos

Vejamos o seguinte exemplo :

Uma empresa contrata um empréstimo de R$ 50.000,00 e prazo de vencimento de 42 meses. Sendo a taxa de juro anual de 22 %. Qual o montante a pagar?

Temos então as seguintes informações:

C = R$ 50.000,00

i= 22 % ao ano

n= 42 meses

M= é o queremos encontrar

Note que temos o período de tempo em meses e a taxa ao ano. Neste caso temos que transformar o período para ano. Como em um ano temos 12 meses teremos:

n= 42/12 = 3,5 anos

Pronto estamos em uma situação de período de tempo não inteiro e exige resolução através de convenção.

Inicialmente iremos resolver através de convenção linear depois utilizando convenção exponencial.

Usando Convenção Linear

Para utilizar convenção linear temos que separar o tempo em uma  parte inteira e outra fracionada.

Neste caso teremos:

n= 3

nfrac= 0,5

Ou seja 3,5 anos = 3 anos + 0,50 anos

Agora podemos substituir os valores na fórmula para calcular  montante utilizando convenção linear vista anteriormente:

Resposta: se utilizarmos convenção linear teremos um montante de R$ 100.779,56

Se ao invés de utilizarmos convenção linear tivéssemos aplicado convenção exponencial, qual seria o valor do montante?

Usando Convenção Exponencial

Neste caso de convenção exponencial iriamos utilizar na equação para encontrar o montante da convenção exponencial n = 3,5 anos, pois tanto a parte fracionada quanto a inteira iria incidir juros compostos.

Substituindo os valores, teríamos:

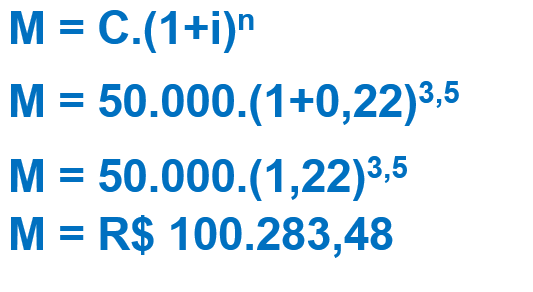
Utilizando convenção exponencial teríamos um montante de R$100.283,48, valor um pouco inferior ao montante utilizando convenção linear.
Veja também

Se você gostou deste texto, compartilhe ele através dos botões sociais logo abaixo, pois isso nos ajuda a continuar a fazer outros artigos como este.

Caso tenha alguma dúvida, comentário ou até mesmo sugestão de novos artigos, por favor entre em contato através do formulário de comentários logo abaixo.

Se você quiser aprender mais sobre matemática financeira, com exemplos passo a passo, indicamos  também que clique na imagem abaixo para conhecer nosso ebook com resolução de problemas de matemática financeira:

 

Muito obrigado pela leitura,

Até breve.