Exercícios Resolvidos Finanças pessoais Juros compostos Matemática financeira Taxas de juros Todos os Artigos do Blog
Taxas equivalentes exercícios resolvidos
Olá, neste artigo vamos resolver alguns exercícios sobre taxas equivalentes usando as fórmulas de conversão de taxa de juros compostos.
Exercício 1 – converter taxa mensal para taxa anual
- Determinar a taxa anual equivalente a 2% ao mês
RESOLUÇÃO
Para calcularmos a taxa equivalente anual de uma taxa mensal precisaremos utilizar a seguinte fórmula de conversão

Substituindo a a taxa mensal por 0,02 poderemos calcular a taxa anual equivalente.
 Assim, podemos afirmar que uma taxa de 26,82 % ao ano é equivalente a uma taxa mensal de 2%.
Assim, podemos afirmar que uma taxa de 26,82 % ao ano é equivalente a uma taxa mensal de 2%.
Exercício 2 – taxa mensal equivalente
2- Determinar a taxa mensal equivalente a 42,5760% ao ano
RESOLUÇÃO
Para calcularmos a taxa equivalente mensal equivalente a uma taxa mensal, situação contrária a anterior, precisaremos utilizar a seguinte fórmula de conversão:

Note que a fórmula de conversão da taxa é a mesma da situação anterior, pois envolve taxa mensal e anual. Todavia, nos cálculos vamos teremos que fazer o cálculo inverso. Veja como ficaria a resolução quando substituirmos a taxa anual por 0,425760:

Assim, podemos afirmar que uma taxa de 3 % ao mês é equivalente a uma taxa anual de 42,5760%.
Exercício 3 – Taxa anual equivalente a taxa diária
3- determinar a taxa anual equivalente a 0,10% ao dia
RESOLUÇÃO
Para calcularmos a taxa equivalente anual de uma taxa mensal precisaremos utilizar a seguinte fórmula de conversão:
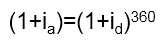
Note que estamos considerando um ano de 350 dias ( ano comercial).
Substituindo a taxa diária por 0,001 e resolvendo, teremos:

Assim, podemos afirmar que uma taxa de 0,1 % ao dia é equivalente a uma taxa anual de 43,31 % se considerarmos ano de 360 dias.
Exercício 4 – taxa equivalente bimestral
4- Determinar a taxa bimestral equivalente a 36,00% em dois anos
RESOLUÇÃO
No cálculo da taxa bimestral equivalente a uma taxa para dois anos teremos que usar a seguinte fórmula:
![]()
Note que ao longo de 2 anos teremos 12 bimestres, por isso o expoente da segunda parte da equação é 12.
Resolvendo para uma taxa de 36 % para dois anos, teremos:

Ou sejam uma taxa de 36% para dois anos é equivalente a uma taxa de 2.59 % ao bimestre.
Veja o vídeo abaixo:
Se você gostou deste artigo, pedimos que compartilhe ele nas suas redes sociais usando os botões abaixo do texto.
Caso tenha alguma dúvida ou até mesmo sugestão, fique a vontade para postar nos comentários logo abaixo.
Veja este outro artigo do blog onde detalhamos as diferenças entre taxas nominais e efetivas:
Visite também nosso canal no youtube.
Muito obrigado!
Até breve!




